Introduction
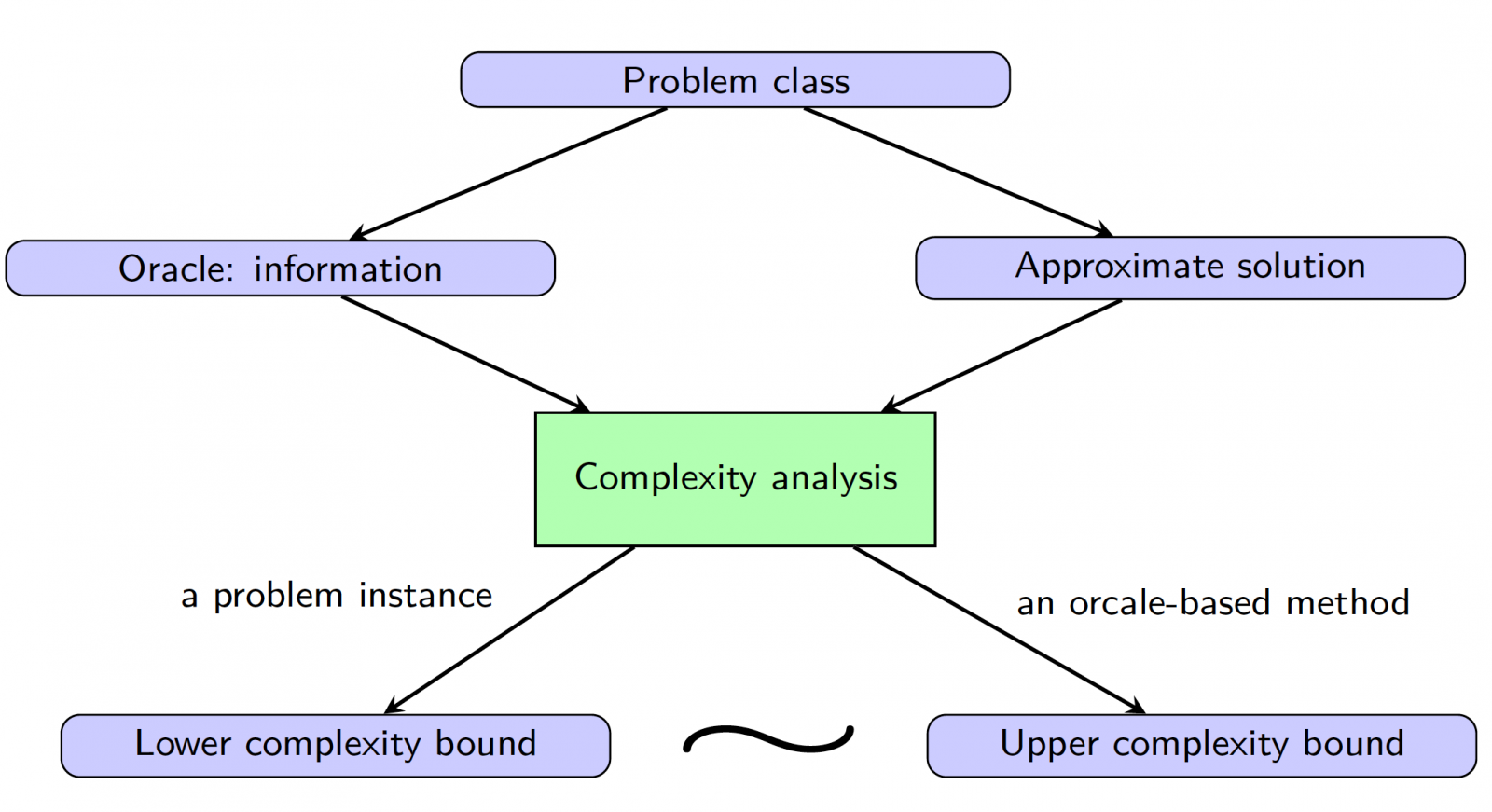
First-order methods (FOMs) or gradient-type methods find a solution of a problem by inquiring gradient and/or function value information. Compared to second-order or even higher-order methods, FOMs generally have much lower per-update complexity and much lower memory requirements. They have been popularly used for solving very large-scale problems that arise from signal processing, imaging, and machine learning. We design various FOMs for structured functional constrained problems, analyze their theoretical properties, and also demonstrate their numerical performance. Through establishing the convergence rate, we show the worst-case complexity bounds of FOMs for solving a class of structured problems, and by constructing worse-case problem instances, we show their information-based lower-complexity bounds. Our goal is to design "optimal" methods, in the sense that their worst-case complexity bound can match with the lower bound. We have worked on accelerated FOMs for linearly constrained problems, inexact augmented Lagrangian methods for nonlinear functional constrained problems, and also FOMs for saddle-point problems.
Affiliated Researchers
- Pin-Yu Chen, IBM Research
- Qihang Lin, University of Iowa
- Yuyuan Ouyang, Clemson University
Current graduate research assistants:
- Zichong Li
Funding Sources
- Division of Mathematical Sciences, National Science Foundation (NSF)
- IBM Research
Resources
Recent publications:
- Z. Li, P. Chen, S. Liu, S. Lu, Y. Xu. Rate-improved Inexact Augmented Lagrangian Method for Constrained Nonconvex Optimization, AISTATS, 130, 2170--2178, 2021.
- Z. Li and Y. Xu. Augmented Lagrangian based first-order methods for convex-constrained programs with weakly-convex objective, INFORMS Journal on Optimization, 3(4):373-397, 2021.
- Y. Xu. First-order methods for constrained convex programming based on linearized augmented Lagrangian function, INFORMS Journal on Optimization, 3(1), 89--117, 2021.
- Q. Lin, R. Ma and Y. Xu. Inexact Proximal-Point Penalty Methods for Non-Convex Optimization with Non-Convex Constraints, 2019.
- Y. Xu. Iteration complexity of inexact augmented Lagrangian methods for constrained convex programming. Mathematical Programming, Series A, 185, 199--244, 2021.
- Y. Ouyang and Y. Xu. Lower complexity bounds of first-order methods for convex-concave bilinear saddle-point problems. Mathematical Programming, Series A 185, 1--35, 2021.
- Y. Xu. Accelerated first-order primal-dual proximal methods for linearly constrained composite convex programming. SIAM Journal on Optimization, 27(3), 1459–1484, 2017.