All Projects
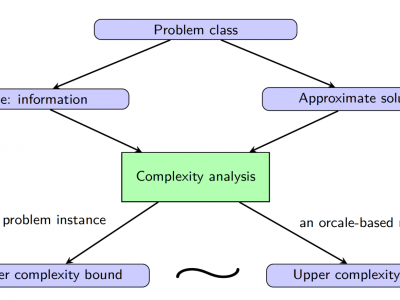
First-order methods for structured large-scale problems
First-order methods (FOMs) or gradient-type methods find a solution of a problem by inquiring gradient and/or function value information. Compared to second-order or even higher-order methods, FOMs generally have much lower per-update complexity and much lower memory requirements.
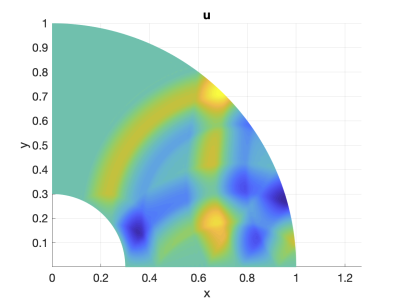
Galerkin Difference Approximations: Robust, Efficient, and High-Order Accurate PDE Discretization
Galerkin Difference (GD) methods are a new class of finite element approximations based on a Galerkin projection into a piecewise polynomial space described by a set of known basis functions.
Fengyan's Project Page
The project introduction will be added shortly.
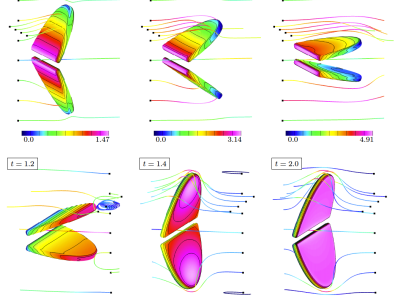
High-Order Accurate Partitioned Algorithms for Fluid-Structure Interactions and Conjugate-Heat Transfer
Fluid-structure interaction (FSI) problems are important in many areas of engineering and applied science such as modeling of blood flow, flow-induced vibrations of structures, and wave energy devices, and there is significant interest in numerical simulation tools for such problems. Conjug
Chjan's project page
The project introduction will be added shortly.
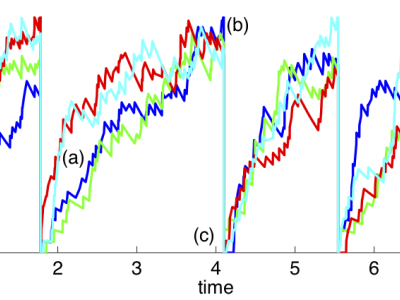
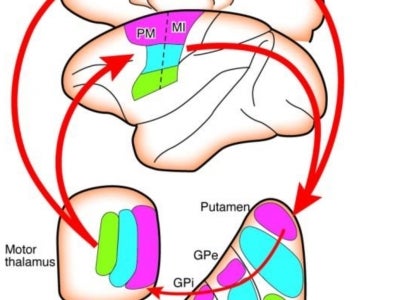
Mathematical Neuroscience
This project concerns developing theoretical models of processing taking place in a number of brain areas, mostly early sensory pathways. One set of problems we have addressed concerns the asynchronous steady state of a sparsely, randomly connected neuronal network. Another
Rongjie's Project Page
The project introduction will be added shortly.
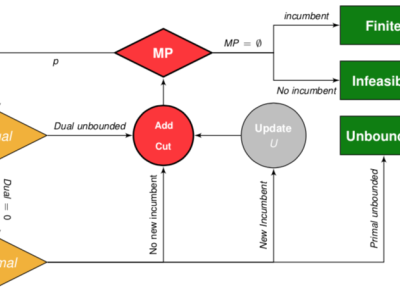
Optimization problems with complementarity constraints
A complementarity constraint requires that one of a pair of variables should be zero. Optimization problems with complementarity constraints are widespread, arising for example in transportation problems, energy optimization, and sparse optimization.
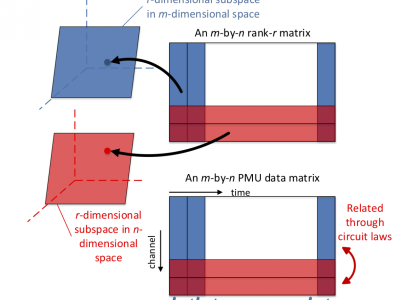
Rank minimization algorithms
We investigate the use of nonconvex approaches to rank minimization problems, an alternative to widely-used convex approaches such as nuclear norm minimization.
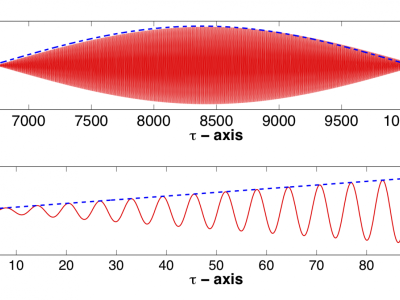
Modeling and Analysis of Wave Amplification in the Cochlea
The fundamental open question in understanding how we hear concerns the role of a nonlinear feedback mechanism known as the cochlear amplifier.
Research Training in Mathematical Modeling, Analysis and Computation
This is an interdisciplinary program for undergraduates, graduate students, and postdoctoral associates that integrates modeling, analysis, and computations with contemporary experimental research.
Advanced Computational Toolkit for Engineered Optical Materials (ACTEOM)
ACTEOM is a DARPA funded project, part of the EXTREME program, with the goal of developing an Advanced Computational Toolkit for Engineered Optical Materials (ACTEOM).