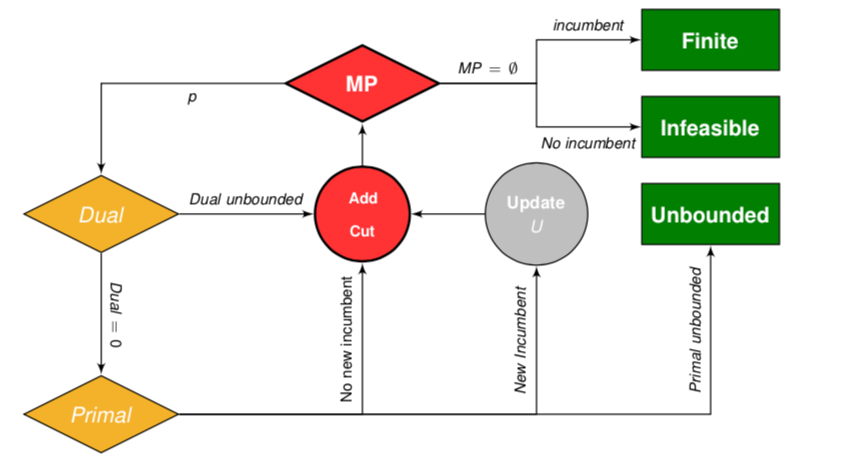
Introduction
A complementarity constraint requires that one of a pair of variables should be zero. Optimization problems with complementarity constraints are widespread, arising for example in transportation problems, energy optimization, and sparse optimization. We have developed methods for solving optimization problems with complementarity constraints to provable global optimality, we have investigated their theoretical structure, and we have also shown how very good solutions to sparse optimization problems can be found using a complementarity formulation and nonlinear programming solvers.
A generalization of complementarity constraints can be used to construct an equivalent continuous lifting of a rank minimization problem.
Affiliated Researchers
- Jong-Shi Pang, USC
- Andreas Wächter, Northwestern
- Xin Shen
- Bin Yu
- Lijie Bai
- Jing Hu
Funding Sources
NSF, AFOSR
Resources
An enhanced logical Benders approach for linear programs with complementarity constraints, Francisco Jara-Moroni, John E. Mitchell, Jong-Shi Pang, and Andreas Wächter. Journal submission. March 2019.
Solving Linear Programs with Complementarity Constraints using Branch-and-Cut, Bin Yu, John E. Mitchell, and Jong-Shi Pang, DOI: 10.1007/s12532-018-0149-2. Mathematical Programming Computation, 11(2), pages 267-310, 2019.
A Penalty Method for Rank Minimization Problems in Symmetric Matrices, Xin Shen and John E. Mitchell. DOI: 10.1007/s10589-018-0010-6. Computational Optimization and Applications, 71(2), pages 353-380, 2018.
Complementarity Formulations of ℓ0-norm Optimization Problems, Mingbin Feng, John E. Mitchell, Jong-Shi Pang, Xin Shen, and Andreas Wächter. Pacific Journal of Optimization, Volume 14, Number 2, 273-305, 2018.
On conic QPCCs, conic QCQPs and completely positive programs, Lijie Bai, John E. Mitchell, and Jong-Shi Pang, Mathematical Programming, 159(1), pages 109-136, 2016.
An algorithm for global solution to bi-parametric linear complementarity constrained linear programs, Yu-Ching Lee, Jong-Shi Pang and John E. Mitchell, , Journal of Global Optimization 62(2), pages 263-297, 2015.
Global resolution of the support vector machine regression parameters selection problem with LPCC, by Yu-Ching Lee, Jong-Shi Pang, and John E. Mitchell. EURO Journal on Computational Optimization, 3(3), pages 197-261, 2015.
Convex Quadratic Relaxations of Nonconvex Quadratically Constrained Quadratic Programs, John E. Mitchell, Jong-Shi Pang, and Bin Yu. Optimization Methods and Software, 29(1), pages 120-136, 2014.
A Globally Convergent Probability-One Homotopy for Linear Programs with Linear Complementarity Constraints, Layne T. Watson, Stephen C. Billups, David R. Easterling and John E. Mitchell. SIAM Journal on Optimization, 23(2), 1167-1188, 2013.
On Convex Quadratic Programs with Linear Complementarity Constraints, Lijie Bai,John E. Mitchell, and Jong-Shi Pang, Computational Optimization and Applications, 54(3), pages 517-554, April 2013.
Obtaining Tighter Relaxations of Mathematical Programs with Complementarity Constraints, John E. Mitchell, Jong-Shi Pang, and Bin Yu. Chapter 1 in Springer Proceedings in Mathematics and Statistics, Volume 21, August 2012.
An LPCC Approach to Nonconvex Quadratic Programs, Jing Hu, John E. Mitchell, and Jong-Shi Pang, Mathematical Programming 133(1-2), pages 243-277, 2012.
On Linear Programs with Linear Complementarity Constraints, Jing Hu, John E. Mitchell, Jong-Shi Pang, and Bin Yu. Journal of Global Optimization, 53(1), pages 29-51, 2012.
On the Global Solution of Linear Programs with Linear Complementarity Constraints, Jing Hu, John E. Mitchell, Jong-Shi Pang, Kristin P. Bennett, and Gautam Kunapuli, SIAM Journal on Optimization 19 (1), 2008, pages 445-471.