Rank minimization algorithms

We investigate the use of nonconvex approaches to rank minimization problems, an alternative to widely-used convex approaches such as nuclear norm minimization. Nonconvex approaches better capture the structure of the problem and may therefore lead to better solutions. It is envisioned that our analysis of the methods we develop will show that they can be successfully applied to a broad range of problems in compressed sensing, low-rank matrix theory, and low-rank tensor analysis.

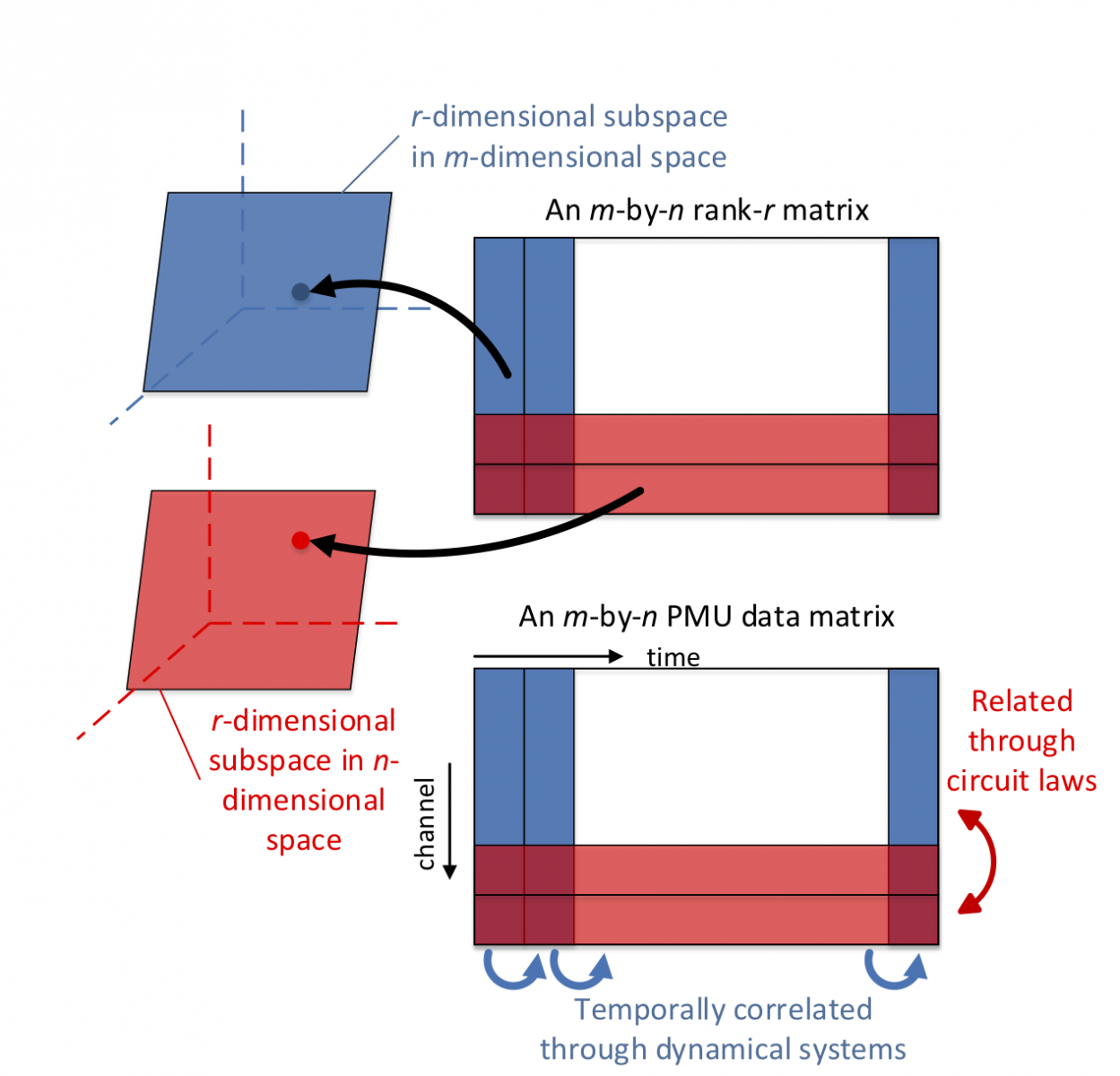
One particular application of particular interest is in power systems. Data scarcity has been a major issue for power system monitoring. The current Supervisory Control and Data Acquisition (SCADA) systems typically provide measurements every 2-4 seconds, offering only a steady state view into the power system behavior. Thanks to the American Recovery and Reinvestment Act of 2009, a large number of phasor measurement units (PMUs) have now been installed and constantly provide huge volumes of data about power system operating conditions and energy demand. To date, two thousand multi-channel PMUs are installed in North America, with an average total cost per PMU as high as $40-180K. PMUs can directly measure bus voltage phasors and line current phasors at synchronized time instants. With data rates of 30 or 60 samples per second, these PMUs produce terabytes of data daily, offering dynamic visibility into the power system.